Size of the diatoms in a chain-like colony II

A surprising relationship between size sequence and dragon curve

On the previous page it was shown that the sequence of differences of length indices of neighboring diatoms in a chain-shaped colony can be calculated according to a simple scheme. For the practical observability of this sequence, synchronicity of the divisions must be assumed. A graphical interpretation of this sequence will be presented here. More details can be found in the publication (3).
As a reminder: If one assumes that the development of the size sequences is started with the axiom L⁰, the sequences of the size indices result from the described L-system to (see also (4)):
g₀ = 0
g₁ = 0 1
g₂ = 0 1 2 1
g₃ = 0 1 2 1 2 3 2 1
g₄ = 0 1 2 1 2 3 2 1 2 3 4 3 2 3 2 1
….
The corresponding difference sequences are:
d₁ = 1
d₂ = 1 1 -1
d₃ = 1 1 -1 1 1 -1 -1
d₄ = 1 1 -1 1 1 -1 -1 1 1 1 -1 -1 1 -1 -1
….

If one would start with j >0 instead of the size index 0, then each index of the size sequence would have to be increased by the value j. The sequences of differences remain unchanged. In (3) it is shown that one can also give a Lindenmayer system (L-system) for the sequences of differences.

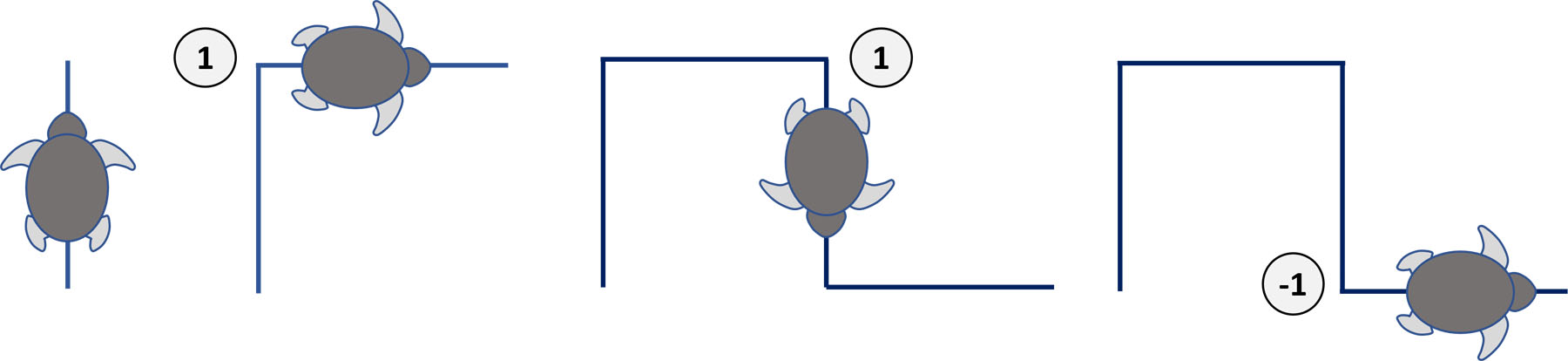
For L-systems, the generated sequences are often visualized by a turtle graphics. Here, the generated sequence (for example) is run through from left to right, and depending on the letter in the sequence, a certain command is executed. Thus, depending on the letter, one can execute a rotation by an angle, raise or lower the pen, change the color, etc. These rules are to be used:

1. Go forward by one length unit.
2. Stop the movement if the end of the sequence is reached.
   Otherwise: Read the next letter, then turn right by 90° for value 1, turn left by 90° for value -1.
3. Go to 1 (jump instruction).

For d4 = 1 1 -1 1 1 -1 -1 1 1 1 -1 -1 1 -1 -1 this figure is obtained:	This video shows the creation of the 6th generation.

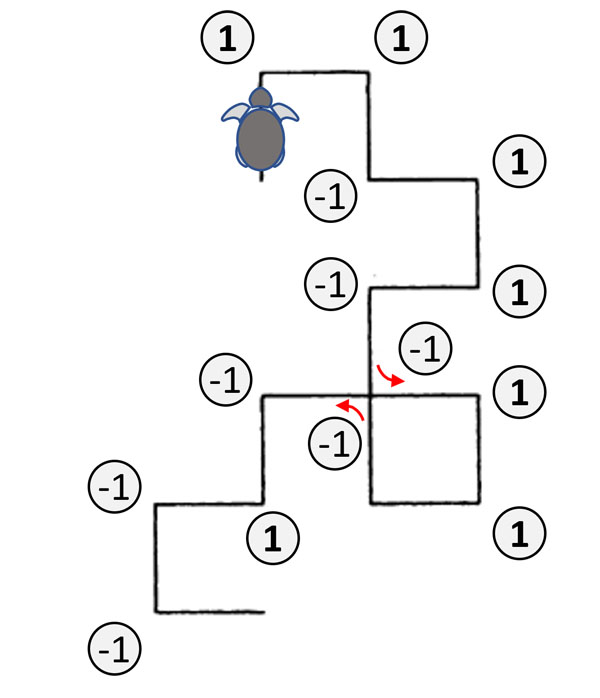These sequences and their visualization are well known. The curves are called (Heighway) dragon curves (Wikipedia). Dragon curves occur in the diatom chains in the sense in which Pascal's triangle occurs, not as a geometric figure but as a mathematical structure.

Dragon curve of the 13th generation. It contains 2¹³ - 1 = 8192 angles.

If a fragment of a diatom colony matches the theoretical sequence, one can generate part of a dragon curve by checking diatom by diatom for differences in length and generating a turtle graphics in the way described. If the considered diatom is larger than the previous one, one performs a right turn (difference = 1), if it is smaller, one performs a left turn (difference = -1). An example of a correct sequence in a Eunotia chain comprising 25 diatoms can be found in (3).

The properties of dragon curves are well studied. Statements about them can be directly applied to diatom colonies. Dragon curves are exact self-similar fractals. It is plane-filling in the limiting case n→∞ (Hausdorff dimension = 2).

The sequences can be made very easily by folding a strip of paper (Wikipedia). This is folded several times in half to the right. Then you unfold the strip and form the bends to right angles.

. 

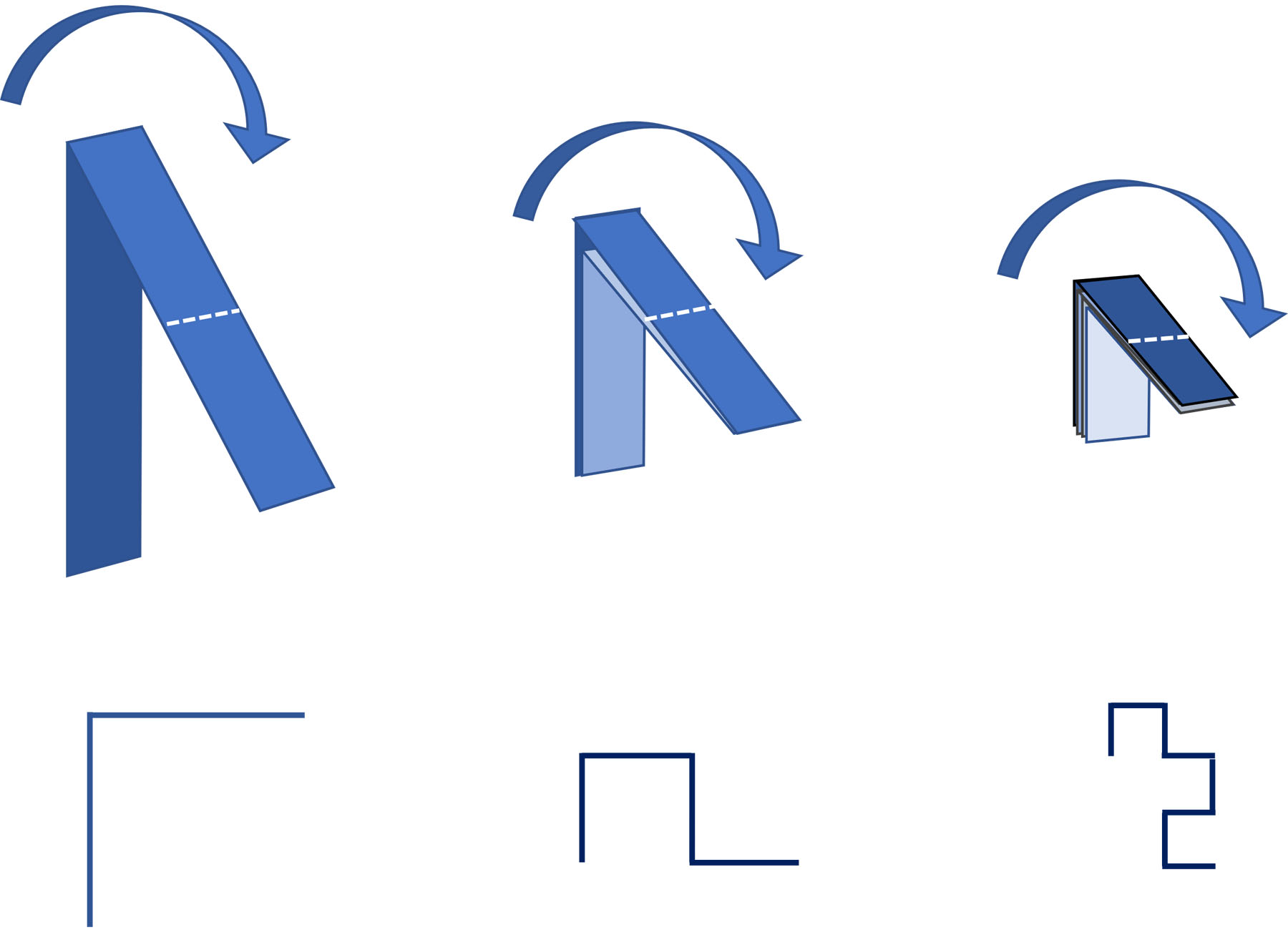
1. Prusinkiewicz, P. and Lindenmayer, A. (1990) The Algorithmic Beauty of Plants. Springer, New York.
2. Benoit B. Mandelbrot  The Fractal Geometry of Nature , Freeman, San Francisco, 1982
3. Harbich, T. (2021), On the Size Sequence of Diatoms in Clonal Chains in Diatom Morphogenesis (Diatoms: Biology and Applications) Vadim V. Annenkov (Editor), Richard Gordon (Editor), Joseph Seckbach (Editor), Wiley-Scrivener; 1. Edition
4. USSING, A.P., GORDON, R., ECTOR, L., BUCZKO´ , K., DESNITSKIY, A.G. & VANLANDINGHAM, S.L. (2005). The colonial diatom ‘‘Bacillaria paradoxa’’: chaotic gliding motility, Lindemeyer Model of colonial morphogenesis, and bibliography, with translation of O.F. Müller (1783), “About a peculiar being in the beach-water”. Diatom Monographs, Vol. 5. Koeltz, Koenigstein, Germany.

• Prev
• Next