Größenfolge der Diatomeen in einer kettenförmigen Kolonie III

Synchronizität

Die wesentliche Voraussetzung für die Korrektheit der Beschreibung durch ein D0L-System ist die synchrone Teilung der Diatomeen, die sicherlich nicht dauerhaft gegeben ist. Es wurde ausgeführt, dass man in der Praxis primär in Kulturen längere kettenförmige Kolonien findet. Eine Überprüfung einer längeren in Kultur gewachsenen Kette dürfte sehr aufwendig und wenig erfolgversprechend sein. Wenn man lediglich die Übereinstimmung von kurzen Fragmenten mit der theoretischen Folge untersucht, sind die Anforderungen an die Synchronizität unter Umständen geringer. Das erste Auftreten eines Fingerabdrucks in der Generation m bedeutet, dass m Generationen erforderlich sind, um das beobachtete Muster erstmals aus einer Zelle zu erzeugen. Auch die Übereinstimmungen in späteren Generationen benötigen genau m Generationen, um aus einer einzigen Zelle hervorzugehen. Es genügt also zur Übereinstimmung mit der theoretischen Folge, wenn die Synchronizität über m Generationen erhalten bleibt. Im Beispiel erscheint der Fingerabdruck zum ersten Mal in der 5. Generation, so dass die relativen Abweichungen in den Generationszeiten weniger als 20% betragen müssen, um das Muster des Fragments zu erhalten.

Bestimmt man bei einem Fragment, das aus L Diatomeen besteht, die Zahl m so, dass 2^m-1 < L ≤ 2^m gilt, dann erscheint das Muster frühestens in der Generation m. Leider kann man sich nicht darauf verlassen. Betrachten wir noch einmal den Baum der Generationen. Aus der ersten Zelle entstehen in der ersten Generation gleichzeitig zwei Tochterzellen. In der n-ten Generation sind aus jeder dieser beiden Zellen 2^n-1 Diatomeen hervorgegangen. Ihnen entsprechen zwei Strings der Länge 2^n-1, die in der Mitte der n-ten Generation aneinander grenzen. Ein Fragment, das Diatomeen aus beiden Hälften in der n-ten Generation enthält, besitzt unterschiedliche Vorfahren in der 1. Generation, also vor n-1 Generationen. Eine synchrone Entwicklung muss dann über n-1 Generationen gegeben sein, um eine Übereinstimmung der Folge der Größen mit der Theorie zu garantieren. Betrachtet man die Entwicklung von Folgen, die aus benachbarten Diatomeen anderer Generationen (>2) entstehen, so findet man auf die gleiche Weise, dass Fragmente in der Generation n unterschiedliche Vorfahren auch vor n-2, n-3, .. ,1 Generationen besitzen können.

Bislang wurden die Ketten aus Diatomeen immer so behandelt, als ob sich alle Diatomeen zeitlich zwischen zwei Teilungen befinden. Erfolgen die Teilungen nicht mehr synchron, muss man damit rechnen, Fragmente zu finden, in denen sich die Diatomeen in unterschiedlichen Teilungsstadien befinden. Immerhin ist dann auf den ersten Blick zu erkennen, dass die Modellierung als Lindenmayer-System seine Grenzen überschritten hat.

Beispiel für Synchronizität über wenige Generationen

Wenn man eine Diatomeenkultur mit einer einzelnen Zelle startet und die Diatomeen in regelmäßigen Abständen auszählt, so kann man häufig beobachten, dass schon nach 3 oder 4 Generationen Abweichungen vom Potenzgesetz 2ⁿ auftreten. Entsprechendes wird man bei kettenförmigen Kolonien erwarten. Das Bild links zeigt eine Probe aus einem kleinen Bach (zum Vergrößern anklicken). Es ist eine noch sehr junge Melosira-Kolonie zu sehen, die sich nach der Bildung einer Auxospore entwickelt hat. Dieser Fund ermöglicht es, die maximale Größe der Diatomeen zu bestimmen, jedoch sind auch hier die Größenunterschiede zwischen den Zellen benachbarter Diatomeen sehr gering. Die Kolonie eignet sich aber gut zur Beobachtung der Synchronizität der Zellteilungen. Sie wurde in ein Kulturgefäß mit Nährlösung überführt, wo sie sich gut entwickelte. Nach drei Tagen bot sich dieses Bild (zum Vergrößern anklicken):

Die Diatomeen weisen unterschiedliche Teilungsstadien auf, wobei eine kleinräumige Ordnung gegeben ist. Die Entwicklung scheint nur über zwei bis drei Generationen synchron zu verlaufen. Noch deutlicher wird dies in einer Zeitrafferaufnahme. Dazu wurde die Kultur über mehrere Tage in der Nähe einer Lampe bei etwa 200 Lux ohne zusätzliche Beleuchtung beobachtet. Verwendet wurde ein einfaches Makroskop, wie es auf der Seite über Geräte zur Beobachtung zu sehen ist. Das Objektiv war ein Zeiss Luminar mit 25 mm Brennweite.

Links ist das entstandene Video in 3600-fachem Zeitraffer zu sehen (Vollbildmodus wird empfohlen). Die Helligkeit schwankt aufgrund wechselnden zusätzlichen Tageslichteinfalls. Die Dunkelpausen im Video entsprechen der Dunkelphase der Beleuchtung (Tageszyklus mit einer Hellphase von etwa 12 Stunden pro Tag). Sie wurden im Video stark verkürzt. In Dunkelheit kommen die Teilungsprozesse zum Stillstand. Es fällt auf, dass an wechselnden mehr oder weniger großen Abschnitten ungeschlechtliche Vermehrung auftritt. Hier dehnt sich die Kette. Zwischen den Zellteilungen liegen größere Zeitabschnitte, in denen von außen bei dieser geringen Auflösung kein Fortschritt festzustellen ist.

Eine ähnliche Beobachtung wurde an einer kultivierten Eunotia sp. gemacht. Links ist ein Video in 7200-fachem Zeitraffer zu sehen. Hier wurde die Kultur über einen Zeitraum von 70 Stunden permanent unter der LED-Beleuchtung des Mikroskops gehalten. Da Eunotia motil ist, können sich Diatomeen von den Enden der Kette und sogar aus Positionen dazwischen entfernen. In Folge der Ausdehnung der Kette kommt es zur Ablösung und Aufwölbung der Kolonie vom Substrat. Wie im Beispiel von Melosira erkennt man lokal unterschiedliche Teilungsstadien und dementsprechend zeitlich unterschiedliche laterale Ausdehnung der Kolonie. In Kulturen kommen jedoch häufig auch sehr lange Ketten mit einheitlicher Struktur vor. Ob hier der Tag-Nacht-Rhythmus eine synchronisierende Wirkung besitzt, ist unklar.

Jenseits des D0L-Systems

Abweichungen der Generationszeit dürften statistischer Natur sein. Je länger sich eine Kolonie entwickelt, umso mehr Abweichungen vom deterministischen Modell sind zu erwarten. Wenn die Synchronizität über maximal k Generationen gegeben ist, werden sich immer Bereiche mit bis zu 2^k Diatomeen finden, die mit dem D0L-System übereinstimmen. Die Anwendbarkeit des Modells ist auf k Generationen beschränkt.

Numerisch kann man Systeme modellieren, bei welcher die Zeit zwischen aufeinanderfolgenden Teilungen eine Zufallskomponente besitzt, aber die Vorhersagekraft eines solches Modells mit stochastischer Komponente ist begrenzt. Vermutlich kann immerhin das allgemeine Verhalten reproduziert werden, wie es im Video der Melosira-Kultur erkennbar ist. Der Ansatz soll kurz skizziert werden. Sobald eine Diatomee durch Teilung entstanden ist, beginnt ein individueller Zeitabschnitt, bis daraus zwei Diatomeen im selben initialen Zustand entstanden sind. Wie beim Pascalschen Dreieck oder der Folge der Generation in der vorgestellten Visualisierung, soll nachfolgend die Zeitachse vertikal von oben nach unten orientiert sein. Die Spitze des Dreiecks repräsentiert eine Diatomee vor ihrer Teilung und die entgegengesetzten Ecken stehen für die Tochterzellen nach abgeschlossener Teilung. Die Höhe des Dreiecks soll proportional zur Dauer des Teilungsvorgangs sein. Je nach Orientierung der Diatomee vor Teilung gibt es diese Möglichkeiten, die den Produktionsregeln entsprechen: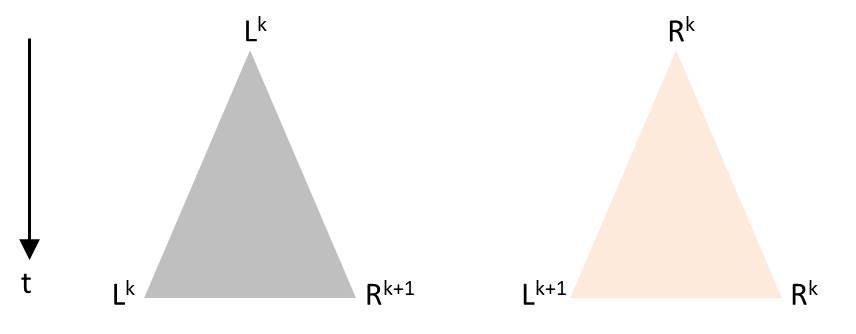

Die Winkel im Dreieck werden so gewählt, dass sich die Dreiecke in der Zeichnung nicht überdecken. Beginnt man wieder mit L0, so könnte zum Beispiel eine solche Abfolge entstehen:

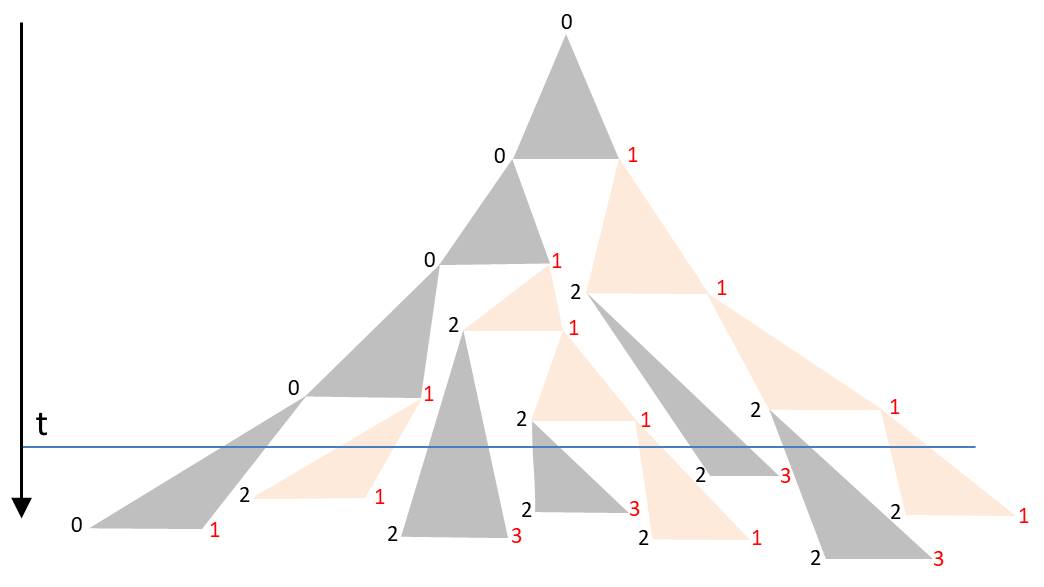
Die Orientierung der Diatomeen wurde wieder durch die Schriftfarbe visualisiert. Die Ecken der Dreiecke bilden einen Binärbaum. Jedem Knoten ist die Dauer der folgenden Zellteilung zugeordnet. Wählt man sie identisch, entsteht das beschriebene D0L-Modell. Je stärker diese Zeitintervalle um die mittlere Generationszeit fluktuieren, desto geringer ist die Synchronizität. Für ein realistisches Modell müsste man durch Beobachtungen die Wahrscheinlichkeitsdichte der Zeiten für Zellteilungen ermitteln. Zudem besteht die Möglichkeit, Abhängigkeiten und Korrelationen zu berücksichtigen. Laney et al. (2012) haben in ihrer Veröffentlichung „Diatoms favor their younger daughters“ nachgewiesen, dass die Tochterzellen der marinen zentrischen Diatomee Ditylum brightwellii unterschiedliche Teilungszeiten besitzen. Diejenige Diatomee, welche die kleinere Hypotheka erbt, zeigt eine schnellere Teilung als ihre Schwester, welche die größere Epitheka übernimmt. Sollte dies auch für die hier betrachteten kettenförmigen Kolonien gelten, würde bereits durch diesen Effekt die Synchronizität verloren gehen.
Zu einer bestimmten Zeit t findet man die Kolonie in einem Zustand vor, der durch die Schnittlinie entlang der Horizontalen charakterisiert ist. Die blaue Linie im Diagramm gibt ein Beispiel. Durch die stark schwankenden Zeiten für Teilungen besteht hier keine alternierende Ausrichtung der Diatomeen. Wie erwähnt, wird die räumliche Trennung der Diatomeen erst im unteren Teil des Dreiecks offensichtlich.

Flexibilität der Ketten und Bruchstellen

Zum Schluss möchte ich mich mit einer Passage aus der Veröffentlichung von Ussing et al. (2005) befassen. Darin heißt es:

“The flexibility of chains, which affects their entanglement (Karp-Boss et al. 1998) might depend on the nonuniformity in size predicted by this model. Smaller cells may also represent weak points in the chain at which it could fragment in a turbulent environment or during predation. So this simple mathematical model may have some life cycle and ecological consequences.”

Bei vielen kettenbildenden Spezies sind die relativen Größenunterschiede zwischen aufeinander folgenden Valven gering. Selbst in dem einigermaßen gut auswertbaren Beispiel der Fragilaria-Kolonie lagen diese bei nur 0,6 %. Die Unterschiede der Valvengrößen sind etwa bei der kultivierten Melosira derartig gering, dass man sie selbst in großen Kolonien kaum wahrnimmt. In einem Fragment, das zum ersten Mal in der Generation m erscheint, unterscheiden sich bei synchroner Teilung der größte und der kleinste Größenindex höchstens um m. Das ist bei den kleinen Fragmenten, die man zumeist antrifft, nicht viel. Bei unserem Beispiel ist m = 5, aber der Unterschied zwischen dem Größenindex von größter und kleinster Diatomee beträgt nur 3. Wie wir gesehen haben, weisen zumindest bei synchronen Teilungen verbundene Diatomeen immer einen Größenunterschied von einem Schritt auf. Von einer „Sollbruchstelle“ kann man deshalb kaum sprechen. Teilen sich die Diatomeen nicht synchron, können Abweichungen von diesen Regeln auftreten. Da sich die Dauer von Zellteilungen nicht um Größenordnungen unterscheiden, kann dies die Verhältnisse nicht drastisch ändern. Den Einfluss der ungleichen Größen der Diatomeen möchte ich nicht in Abrede stellen, aber auch nicht überbewerten.

Karp-Boss, L. & Jumars, P. A. (1998). Motion of diatom chains in steady shear flow. Limnol. Oceanogr., 43, 1767-1773

S R Laney, R J Olson and H M Sosik, Diatoms favor their younger daughters, Limnology and Oceanography, Vol.57, No.5, pp.1572–1578, 2012.

USSING, A.P., GORDON, R., ECTOR, L., BUCZKO´ , K., DESNITSKIY, A.G. & VANLANDINGHAM, S.L. (2005). The colonial diatom ‘‘Bacillaria paradoxa’’: chaotic gliding motility, Lindemeyer Model of colonial morphogenesis, and bibliography, with translation of O.F. Müller (1783), “About a peculiar being in the beach-water”. Diatom Monographs, Vol. 5. Koeltz, Koenigstein, Germany.

• Zurück
• Weiter