Größenfolge der Diatomeen in einer kettenförmigen Kolonie I
In diesem Beitrag soll es um die Frage gehen, welche Größenfolge Diatomeen in einer solchen Kultur besitzen und ob man diese beobachten kann.
| Hinweis: |
Eine genauere Analyse zur Größenfolge von Diatomeen in kettenförmigen Kolonien wird in dieser Veröffentlichung gegeben:
Harbich, T. (2021), On the Size Sequence of Diatoms in Clonal Chains. In Diatom Morphogenesis (Diatoms: Biology and Applications) Vadim V. Annenkov (Editor), Richard Gordon (Editor), Joseph Seckbach (Editor), Wiley-Scrivener; First published: 29 October 2021, https://doi.org/10.1002/9781119488170.ch3 Die mathematischen Aspekte werden in dem Paper formaler als hier behandelt. Als Beispiele für ausgemessene Folgen dient Eunotia sp. Ferner wird eine Faustformel für den Verlust der Synchronizität abgeleitet. |
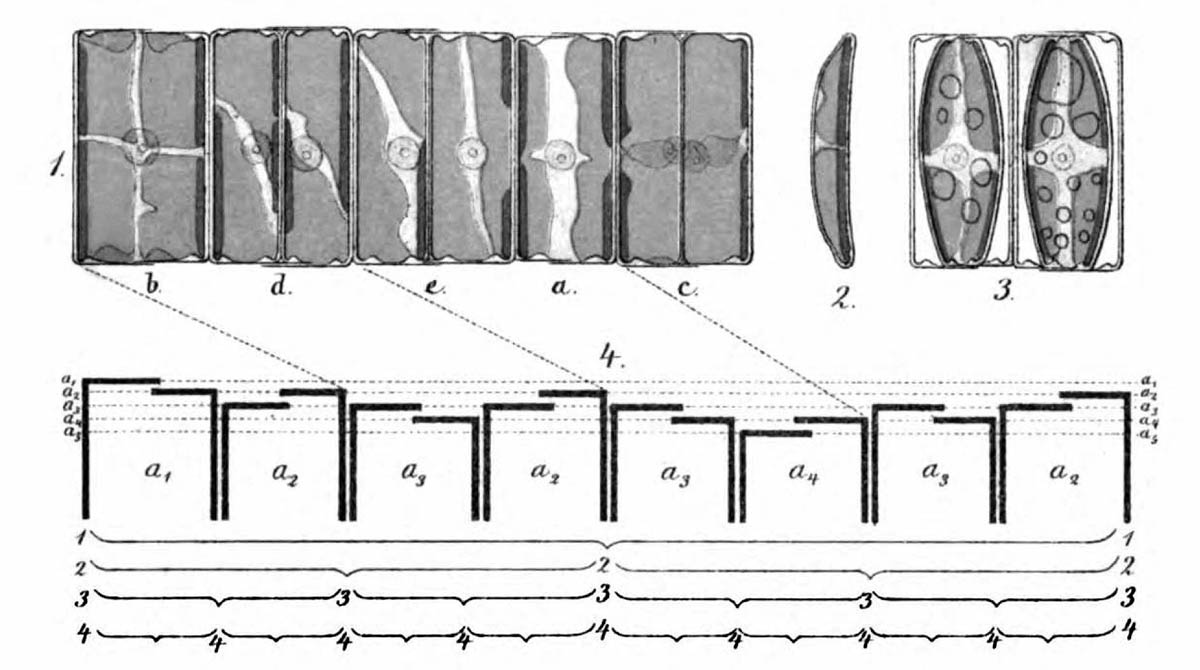
Bereits Pfitzer 1871 stellte die sukzessive Größenverkleinerung am Beispiel einer kurzen Kette aus Diatomeen der Gattung Eunotia dar (siehe Abbildung oben). Konkret soll versucht werden, mögliche Positionen eines Fragments einer solchen Kolonie in der theoretischen Größenfolge zu bestimmen. Dazu muss zunächst die Folge der Größen und der Ausrichtungen der Diatomeen in einer kettenförmigen klonalen Kolonie bekannt sein. Ussing et al. (2005) haben ausgeführt, dass das Bildungsgesetz für diese Folge durch ein eindimensionales Lindenmayer-Model (siehe Lindenmeyer, A. (1968)) beschrieben werden kann, wie es bereits erfolgreich für verschiedene Spezies (z. B. Cyanobakterium Anabaena catenula) verwendet wurde.
Sowohl das Ausmessen der Größe von Diatomeen als auch die Zuordnung zur theoretischen Folge erweisen sich als keine leichte Aufgabe. Eine genauere Betrachtung des Lindenmayer-Systems für kettenförmige Kolonien von Diatomeen ermöglicht es, ein Beispiel aus der Natur erfolgreich zu analysieren. Dies gelingt vermutlich nicht bei jeder Spezies. Man kann auch nicht davon ausgehen, dass eine gefundene Zuordnung eindeutig ist. Nachfolgend werden die mathematischen Grundlagen gelegt und die praktischen Herausforderungen beschrieben. Danach wird die mathematische Methode zur Analyse vorgestellt und an einem Beispiel demonstriert. Wer es also genauer wissen will, findet nachfolgend die Details.
Beschreibung der Größenfolge
Vorbemerkung zur ungeschlechtlichen Vermehrung
Die ungeschlechtliche Vermehrung von Diatomeen wurde bereits in der Einführung kurz dargestellt. Bei jeder Zellteilung entstehen eine Diatomee gleicher Größe und eine kleinere Diatomee. Nachfolgend werden die möglichen Größen der größeren Valve durch fortlaufende Zahlen k bezeichnet, wobei k = 0 der größten möglichen Diatomee und kmax der kleinsten entspreche. Ausgehend von einer Zelle maximaler Größe (Generation 0) existieren in der Generation n
![]()
Diatomeen der Größe k (Animation in der Einführung zeigt ein Pascalsches Dreieck). Die Anwendbarkeit der Formel setzt die Synchronizität der Teilungen voraus und gilt nur bis zum Erreichen der kleinstmöglichen Zelle. Normiert man für eine Generation n die Ergebnisse auf den Wert 1, so erhält man die Wahrscheinlichkeits-funktion zur Binomialverteilung (Wahrscheinlichkeit p = ½). In einer solchen modellhaften Kultur liegt aber keine Wahrscheinlichkeitsverteilung der Diatomeengrößen vor, sondern die Anzahl der Diatomeen einer bestimmten Größe ist deterministisch. Entnimmt man Stichproben, so genügen sie der Binomialverteilung.
Lindenmayer-System
Nun soll die Modellierung der Kolonie durch ein Lindenmayer-System vorgestellt werden. Ein Lindenmayer-System ist ein Tripel D = (A, P, ω), welches aus einem Alphabet A, Ersetzungsregeln P und einem Axiom (Startbedingung) besteht. Die Elemente des Alphabets sollen die Ausrichtung und Größe der Diatomeen in einer Kolonie beschreiben. Eine Kolonie oder ein Fragment davon wird durch einen String aus Zeichen des Alphabets charakterisiert. Die Ersetzungsregeln P geben an, wie sich dieser String von Generation zu Generation ändert. Eine Startbedingung ω, das so genannte Axiom, legt fest, mit welchem String man die Berechnung beginnt.
Alphabet A:
Man stelle sich die Kolonie wie eine Buchstabenfolge (ein String) horizontal geschrieben vor. Die nachfolgend verwendete Notation für die Zeichen der Kette wurde von Ussing et al. (2005) übernommen. Eine Diatomee, deren linke Valve größer als die rechte ist und deren größere Valve durch den Größenindex k gegeben ist, werde mit Lk bezeichnet.
Grafische Darstellung von Lk: ![]()
Entsprechend werde eine Diatomee, deren rechte Valve größer als die linke ist und deren größere Valve durch den Größenindex k gegeben sei, mit Rk bezeichnet.
Grafische Darstellung von Rk:![]()
Lk und Rk gehen durch rechts-links-Spiegelung auseinander hervor.
Das Alphabet besteht aus der Vereinigung der Mengen { Lk | k = 0, 1, 2, … kmax } und
{ Rk | k = 0, 1, 2, … kmax }.
Ersetzungsregeln (Produktionsregeln/ production rules):
Teilt sich eine Diatomee, die durch das Element Lk gekennzeichnet ist, so entstehen zwei Diatomeen in dieser Anordnung:
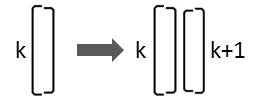
Folglich muss folgende Ersetzung durchgeführt werden:
Lk → Lk Rk+1
Liegt die größere Valve der Diatomee auf ihrer rechten Seite, so ist sie lediglich anders zum Betrachter orientiert:
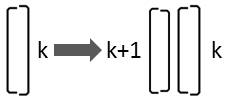
Es ergibt sich durch Spiegelung die Ersetzungsregel:
Rk → Lk+1 Rk
Man setzt voraus, dass die Teilungen synchron erfolgen. Beim Übergang von einer Generation zur nächsten Generation müssen alle Elemente entsprechend dieser Regeln ersetzt werden, so dass sich die Anzahl der Diatomeen verdoppelt. Die erzeugten Strings entsprechen Momentaufnahmen zwischen den Teilungen.
Mit diesen Ersetzungs- oder Produktionsregeln ist das Lindenmayer-Systemen deterministisch und kontextfrei und wird als D0L-System bezeichnet.
Axiom:
Als Axiom (Startwert) wähle ich eine einzelne Zelle mit maximaler Größe, die dem Status nach der sexuellen Reproduktion entspricht. Da die Lage der Zelle beliebig ist, kann als Axiom ω = L0 gewählt werden. Ussing et al. (2005) verwenden ω = R0, was zu gespiegelten, also invertierten Ketten führt. Aus praktischen Gründen, die später erklärt werden, bevorzuge ich L0. In Zusammenhang mit den Eigenschaften der erzeugten Ketten wird auch ihre Abhängigkeit vom Axiom zu diskutieren sein.
Beginnend mit dem Axiom werden iterativ die Produktionen auf alle Elemente des Strings parallel angewandt. So entsteht eine Folge von Strings Gi, welche die Kolonie nach der i-ten Iteration beschreibt, was gerade der i-ten Generation entspricht.
G0 = ω = L0
G1 = L0 R1
G2 = L0 R1 L2 R1
G3 = L0 R1 L2 R1 L2 R3 L2 R1
etc.
Nachfolgend werde ich vereinfachend den String, der nach n Iterationen entsteht, als „n-te Generation“ bezeichnen.
Beobachtung und Herausforderungen
Da das Gesetz von Pfitzer und MacDonald vielfach nachgewiesen wurde und die Beschreibung kettenförmiger Kolonien sich allein auf diese Regel stützt, sollte ein Nachweis der Größenfolge auf den ersten Blick nicht schwierig sein. Dennoch musste ich feststellen, dass dies keineswegs der Fall ist. Dabei zeigen sich folgende Schwierigkeiten:
- Fehlende Zuordnung von Größen zum Größenindex: Beim Ausmessen einer Valven-Größe verfügt man in der Regel nicht über eine Möglichkeit, diese Messgröße dem oben eingeführten Größenindex zuzuordnen. Insbesondere ist die Länge der größten möglichen Valve nicht bekannt.
- Zu kurze Ketten: Selbst, wenn ein Fragment, das nur aus wenigen Diatomeen besteht, gut ausgemessen werden kann, so ist eine Übereinstimmung mit einer theoretischen Größenfolge nur von begrenztem Nutzen. Sie könnte auf Zufall beruhen.
- Abgestorbene Zellen im Fragment.
- Geringe Größenunterschiede der Valven: Die Vorstellung von deutlich ineinander liegenden Valven trifft für viele kettenförmige Kolonien bildende Diatomeen möglicherweise nicht zu. Vielmehr scheinen sich die Valven nur um einen Bruchteil der Valvendicke zu unterscheiden. Auch natürliche Schwankungen in der Größe der Valven könnten eine Rolle spielen. Eine ausreichend genaue Auswertung der Größenfolge der oben gezeigten Melosira-Kolonie war mir nicht möglich.
Die zuletzt genannte Schwierigkeit könnte möglicherweise durch den Einsatz der Rasterelektronenmikroskopie überwunden werden. Auch, wenn all diese Herausforderungen gemeistert sind, bleibt die Frage, ob die Zellteilungen, die zum ganzen Fragment geführt haben, wirklich synchron erfolgten.
Bei der Untersuchung der Längen einer Eunotia sp. führte die Motilität der Diatomeen zu weiteren Problemen. Fragmente aus mehreren Diatomeen können sich von der Kolonie abtrennen. Einzelne Diatomeen wandern häufig von den Enden der Kette weg und auch innerhalb der Kolonie können sich Diatomeen lösen und sich entfernen. Eine solche Lücke schließt sich manchmal in Folge der Ausdehnung durch Zellteilung wieder, so dass die Veränderung unentdeckt bleibt. Das nachfolgende Video unten links zeigt in 1500-fachem Zeitraffer mehrere solcher Ereignisse. Zeitlich weiter auseinander liegende Szenen sind durch eine Dunkelpause unterbrochen. Überraschenderweise kommt es sogar vor, dass sich eine Diatomee an das Ende einer Kette anschließt, wie dies im Video (1500-facher Zeitraffer) rechts unten (in der Nähe des linken Bildrands) zu sehen ist. Einzelne freie Diatomeen setzen sich nach einiger Zeit fest und begründen eine Kolonie, indem sie sich teilen. Es sei erwähnt, dass diese Beobachtungen an Kulturen mit dem inversen Mikroskop durchgeführt wurden. Die Beleuchtung (LED) des Mikroskops ersetzt das Tageslicht. In Dunkeln kommt die Bewegung der Eunotia zur Ruhe.
Ussing et al. (2005) behandeln die Größenfolge vor dem Hintergrund von Untersuchungen an Bacillaria paradoxa, aber es fehlt jeglicher Hinweis, ob versucht wurde, diese Gesetzmäßigkeit zu beobachten und ob dies erfolgreich war.
Durch Zufall stieß ich im Internet auf der Seite (http://www.wunderkanone.de/ ) auf ein hervorragendes Bild einer Fragilaria-Kolonie, das sich auf den ersten Blick als Untersuchungsobjekt anbietet. Das Bild ist nachfolgend mit freundlicher Genehmigung von Hr. Eckhard Völcker (Homepage: http://www.penard.de/ ) wiedergegeben.

Jede der Diatomeen weist deutliche Größenunterschiede zwischen ihren Valven auf, was sich in der unregelmäßigen oberen und unteren Kante bemerkbar macht. Insgesamt beinhaltet das Fragment 14 Diatomeen. Eine recht weit fortgeschrittene Bruchstelle zeichnet sich zwischen der 6. und 7. Diatomee von links ab.
Eine Möglichkeit, die Größen der Diatomeen einem Größenindex zuzuordnen, ist nicht gegeben. Um dennoch die Übereinstimmung mit der Theorie prüfen zu können, erweist es sich als nützlich, die Eigenschaften dieses Lindenmayer-Systems genauer zu untersuchen. Deshalb kehre ich nachfolgend zur Theorie zurück.
Eigenschaften des Lindenmayer-Systems
Zwei einfache Regeln dieses D0L-Systems erweisen sich als besonders wichtig:
Symmetrie:
Eine Kette von Diatomeen wird durch eine Zeichenkette mit Buchstaben des Alphabets Lk und Rk mit
K = 0 .. kmax charakterisiert. Wenn man sie gespiegelt betrachtet, so dass rechts und links vertauscht werden, so muss der entsprechende String in seiner Reihenfolge umgekehrt, also invertiert werden. Zudem muss jedes L durch ein R und jedes R durch ein L ersetzt werden, damit auch die Orientierung jeder Diatomee geändert wird. Der Operator der Spiegelung sei mit S bezeichnet. Die Produktionsregeln (Operator P) sind durch ihre Konstruktion invariant unter Spiegelung, so dass P∘S = S∘P gilt. Es ist gleichgültig, ob man zuerst eine Spiegelung und dann eine Iteration ausführt oder umgekehrt. Anschaulich bedeutet das einfach, dass es bei der Entwicklung einer kettenförmigen Kolonie nicht darauf ankommt, aus welcher Richtung man sie betrachtet.
Änderung des Größenindex:
Es ist hilfreich, die bei Anwendungen der Produktionen des beschriebenen D0L-Systems erzeugten Strings in Abhängigkeit von der Startbedingung zu betrachten. Gemäß der Produktionsregeln entstehen bei ungeschlechtlicher Vermehrung aus einer Diatomee der Größe k eine Diatomee mit Größenindex k und eine kleinere mit Größenindex k+1. Startet man mit dem Axiom Lk anstatt L0 wobei k > 0 sei, so werden in der ersten Generation gemäß der Ersetzungsregeln alle Größenindices um den Wert k erhöht. Entsprechend gilt dies auch in der zweiten und allen weiteren Generationen.
Beobachtet man also die Bildung von zwei Kolonien ausgehend von einzelnen Diatomeen mit unterschiedlichen Größenindices, so entstehen ähnliche Muster in der Größenfolge, wobei jedoch der Größenindex jeder Diatomee in einer Kette um einen konstanten Wert gegenüber der anderen Kette verschoben ist. Bildet man die Differenzen der Größenindices aufeinander folgender Diatomeen, so sind diese Differenzen bei beiden Ketten identisch. Dies bildet den Grundgedanken bei der Beantwortung der Frage, in wie weit man ohne Kenntnis der Zuordnung von Größenindices zu absoluten Längen ein Fragment einer Kolonie in eine theoretische Größenfolge einordnen kann.
Alternative Formulierung
Diese beiden Regeln ermöglichen, eine alternative Formulierung für die Berechnung der Generationen abzuleiten. Im nachfolgenden Bild sind die ersten 5 Generationen ausgehend vom Startwert in Zeilen untereinander angeordnet. Die Zahlen bezeichnen die Größenindices. Zur Vereinfachung der Notation wurde die Ausrichtung der Diatomeen durch die Schriftfarbe gekennzeichnet. Schwarze Ziffern stehen für „L“, rote für „R“.
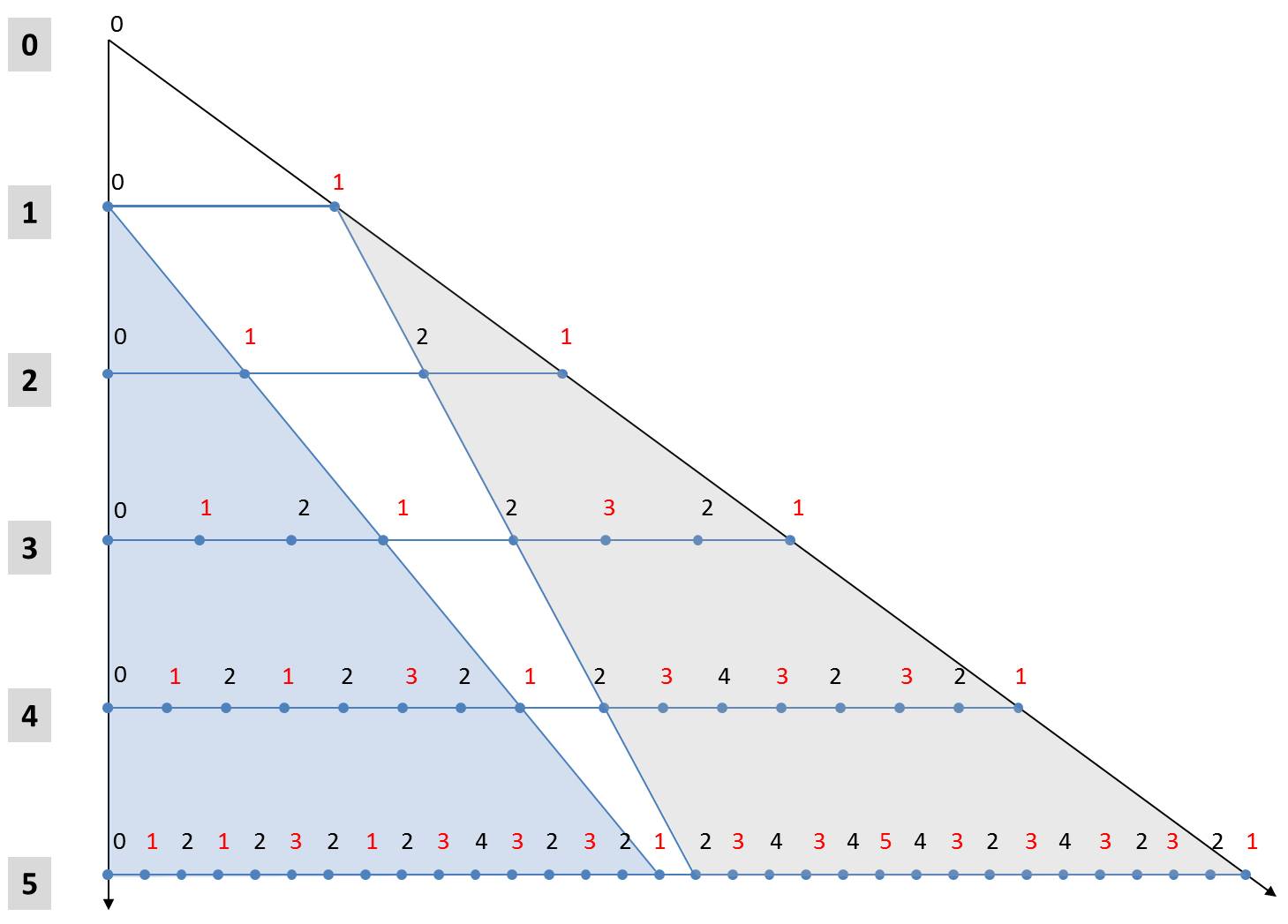
Die 5. Generation ist mit ihren 25 Elementen in der letzten Zeile zu sehen. Das hellblau eingezeichnete Dreieck zeigt, dass seine ersten 24 Elemente gleich der 4. Generation zum Axioms L0 sind. Entsprechendes gilt offenbar auch für alle anderen Iterationen ab der ersten Iteration. Jeweils die erste Hälfte der n-ten Generation ist identisch mit der (n-1)-sten Generation zum selben Startwert L0.
Ein wenig komplizierter ist die Regel für die 2n-1 Elemente der zweiten Hälfte der Generation. Aus dem grauen Dreieck entnimmt man, dass die zweite Hälfte der n-ten Generation die n-1-ste Generation ausgehend vom Startelement R1 ist. Zur Bestimmung der zugehörigen Elemente kann man die beiden oben genannten Regeln anwenden. Alle Elemente der n-1-sten Generation zum Startelement R1 sind um den Wert 1 höher als diejenigen zu einem hypothetischen Startwert R0. Zudem sind sie gespiegelt im Vergleich zu einer Generation, die vom Startelement L1 ausgeht. Man kann die Werte der zweiten Hälfte der n-ten Generation also durch Spiegelung (Austausch von „L“ und „R“ und invertieren der Reihenfolge) und Inkrementieren aller Größenindices aus der (n-1)-ten Generation zum Startwert L0 gewinnen. Letzteres ist gerade identisch mit der ersten Hälfte der n-ten Generation.
Diese Darstellung liefert ein einfaches Schema zur Ermittlung der Generationen. Wenn eine Generation vorliegt, so kann die nächst höhere Generation durch das nachfolgende Schema niedergeschrieben werden, ohne dass man die Ersetzungsregeln explizit verwendet:
- Die vorliegende Generation bildet die erste Hälfte der nachfolgenden Generation.
- Die zweite Hälfte der folgenden Generation erhält man durch Spiegelung (Austausch von „L“ und „R“ und invertieren der Reihenfolge) der vorliegenden Generation mit gleichzeitiger Erhöhung aller Größenindices um den Wert 1.
In jeder Generation alternieren die Orientierungen (Anmerkung zum Beweis wird weiter unten gegeben), so dass man sich auf die Größenindices beschränken kann. Das vereinfachte Schema ist nachfolgend illustriert:
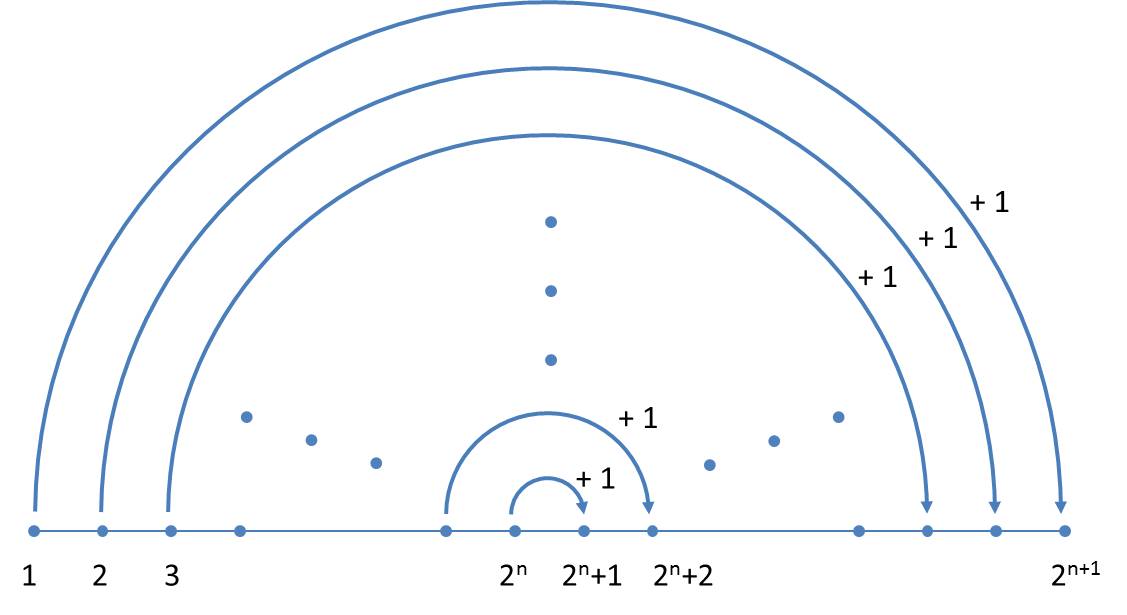
Jetzt wird ersichtlich, warum hier im Gegensatz zu Ussing et al. (2005) ein gespiegeltes Axiom verwendet wird. Da wir von links nach rechts schreiben, kann zur Ermittlung der nächsten Generation immer am Ende ergänzt werden.
Bezeichnet man die Größenindices der n-ten Generation mit ain, wobei i die Werte 1 … 2n annimmt, so lautet das Bildungsgesetz:
![]()
Der Startwert entsprechend dem gewählten Axiom ist a10 = 0. Ein formaler mathematischer Beweis wird in der oben zitierten Veröffentlichung „On the size sequence of diatoms in clonal chains“ gegeben.
Kennt man von einem gefundenen Fragment einer Kolonie die absoluten Indizes der Größe, so kann man die Generation suchen, bei der dieses oder das gespiegelte Muster erstmals auftaucht. Alle nachfolgenden Generationen enthalten dasselbe Muster, so dass es keine eindeutige Zuordnung zu einer Generation geben kann.
Diese Darstellung erlaubt nicht nur die schnelle manuelle Berechnung der Generationen, sondern liefert sofort einige mathematische Einsichten. Zum Beispiel kann wegen des Inkrementierens keine periodische Folge entstehen.
Die wiederholte Verdoppelung mit Spiegelung erzeugt eine selbstähnliche fraktale Struktur. Im nachfolgenden Bild sind Diagramme der Größenindices für die 8. bis 11. Generation gezeigt. Jedes Diagramm bildet die erste Hälfte des darunter befindlichen Diagramms.
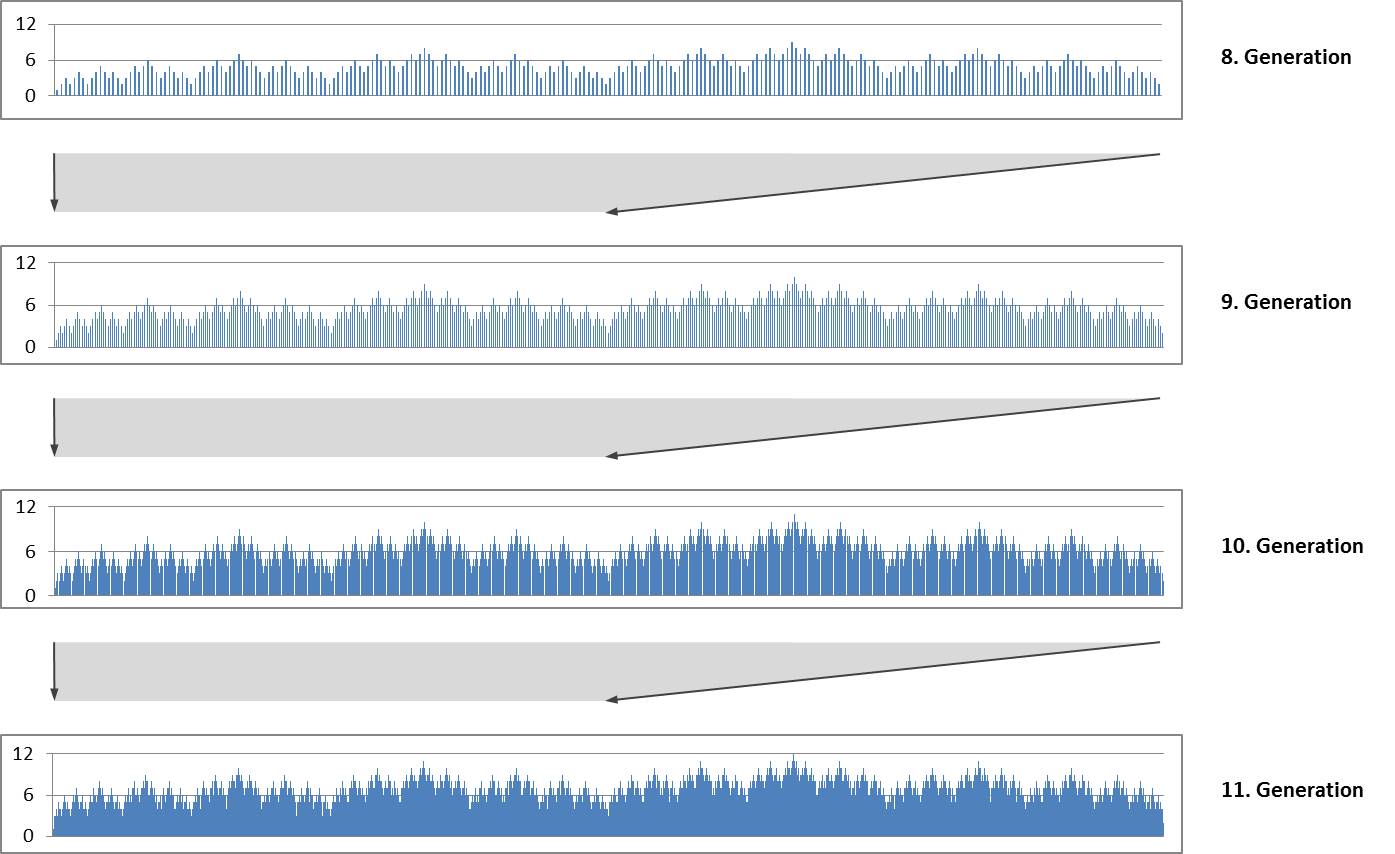
Die Selbstähnlichkeit und fraktale Struktur überraschen nicht, denn sie sind typisch für Lindenmayer-Systeme.
Beim Inkrementieren entsteht aus dem bislang maximalen Größenindex der nächste maximale Größenindex. In Übereinstimmung mit dem Pascalschen Dreieck ist der maximale Wert in der n-ten Generation gerade n. Für seine Position im String lässt sich leicht eine Beziehung formulieren. Im Limes n → ∞ konvergiert die Position gegen 2/3 der Länge des Strings.
Wichtiger für unsere Zwecke sind die folgenden Aussagen, die ab der 1. Generation für jede folgende Generation gelten:
- Die Orientierungen der Diatomeen alternieren.
- Die Differenzen aufeinanderfolgender Größenindices (Größenindex eines Elements – Größenindex seines Vorgängers) können nur die Werte +1 oder -1 annehmen.
Beide Behauptungen lassen sich in wenigen Zeilen durch vollständige Induktion beweisen. Den ersten Satz kann man alternativ sofort aus den Ersetzungsregeln ersehen. Als Induktionsanfang dient die 1. Generation. Beim Induktionsschritt betrachtet man die obere Hälfte der n+1-sten Generation, sowie die Stelle, an der die Hälften aneinander grenzen. Die erste Hälfte der n-ten Generation muss nicht näher betrachtet werden, da sie die (n-1)-Generation darstellt (Induktionsvoraussetzung). Der zweite Satz erweist sich als nützlich für die Charakterisierung eines Fragments.
Die Differenzfolge benachbarter Elemente in der n-ten Generation enthält n-1 Elemente. Sie sind unabhängig davon, welcher Größenindex im Axiom verwendet wurde. Auch für die Bildung der Differenzfolge lässt sich ein einfaches Schema angeben, das unmittelbar aus dem Schema für die Größenindices folgt. Beim Übergang zur nächsten Generation hängt man an die vorhandene Generation zunächst eine 1 und spiegelt dann die vorhandene Generation, wobei man alle Werte invertiert:
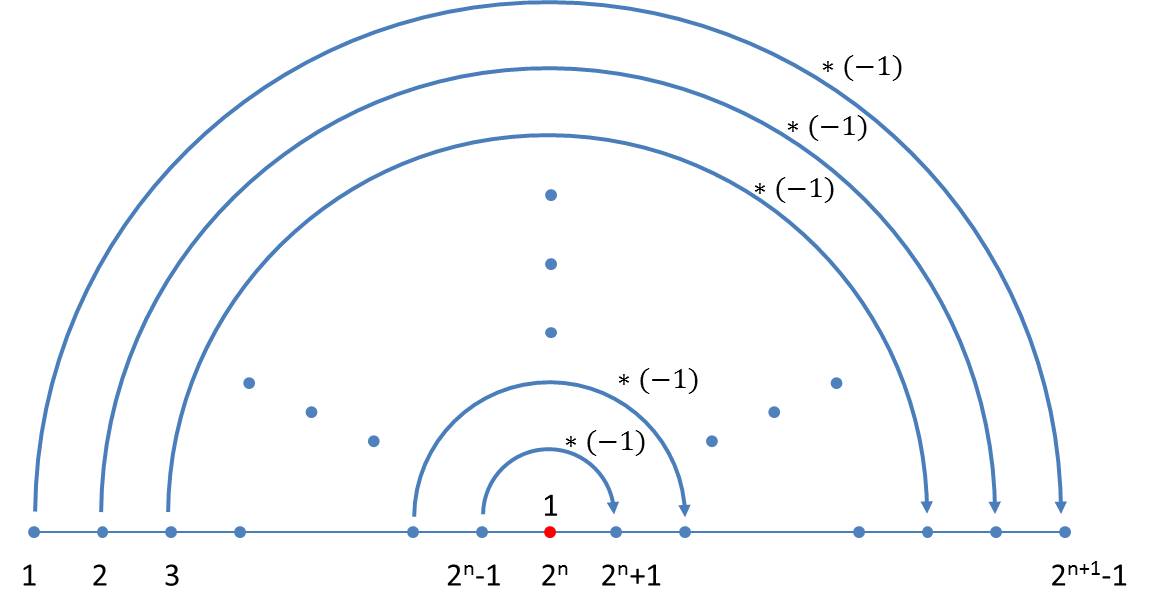
Bezeichnet man die Differenzen zwischen den Größenindices der n-ten Generation mit din, wobei i die Werte 1 … 2n – 1 annimmt, so lautet die Iteration:
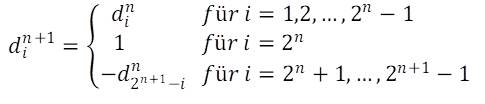
Da die Iteration mindestens eine Differenz erfordert, beginnt man mit dem Startwert d11= 1.
Auswertung der Längen des Fragments
Es ist an der Zeit, zur Analyse des oben dargestellten Fragments von der Fragilaria-Kolonie zurückzukehren. Zunächst einmal erkennt man, dass die Orientierung der Diatomeen in Übereinstimmung mit der Theorie alternierend ist.
Im Bild links wurden aus dem Gesamtbild zu jeder Diatomee an ihrer längeren Valve schmale Streifen herausgeschnitten und nebeneinandergestellt (zum Vergrößern anklicken). Obwohl dies ein Beispiel für eine gute Unterscheidbarkeit der Längen ist, sind diese doch relativ gering. Im Mittel betragen Längenunterschiede zwischen benachbarten Diatomeen etwa 0,6 % ihrer mittleren Länge. Die Beträge der Längenunterschiede benachbarter Diatomeen sind aufgrund der begrenzten Auflösung und vermutlich auch natürlicher Unregelmäßigkeiten nicht konstant. Kleine Justierungen der Marken wirken sich angesichts der sehr geringen Unterschiede stark aus.
Das Balkendiagramm darunter zeigt die Beträge der Längenunterschiede benachbarter Diatomeen (in Prozent der mittleren Zelllänge) und ist durchaus kritisch zu betrachten. Das größte Problem ist der 10. Wert, der extrem von den anderen Werten abweicht. Ansonsten kommen keine Längenunterschiede vor, die sich von den anderen um den Faktor 2 oder 3 unterscheiden. Wenn man es trotz dieses stark abweichenden Wertes als plausibel ansieht, dass das dargestellt D0L-System im Grundsatz korrekt ist, lässt sich die Größenfolge der Diatomeen bis auf eine additive Konstante analysieren. Man betrachtet nur die Eigenschaft, ob eine Diatomee länger oder kürzer als ihr Vorgänger ist.Ist sie länger, wird als Differenz des Größenindex -1, ansonsten 1 notiert. Der 10. Wert (-1) ist wegen der genannten Anomalie als nicht gesichert zu betrachten. Im Bild oben sind diese Differenzen eingetragen. Da, wie mehrfach erwähnt, eine Zuordnung zum absoluten Größenindex fehlt, betrachte ich die Folge -1 1 1 -1 -1 -1 1 1 -1 -1 1 -1 -1 als „Fingerabdruck“ des Fragments der Kolonie.
Nun kann man prüfen, ob der Fingerabdruck sich in einer ausreichend langen Differenzfolge finden lässt. Bei einer Länge des Fragments von 14 Diatomeen, also 13 Längendifferenzen kann er frühestens in der 4. Generation auftreten. Man findet ihn gespiegelt und invertiert in dieser Generation (1 1 -1 1 1 -1 -1 1 1 1 -1 -1 1). Hier ist die Folge der Differenzen zur 4. Generation zu sehen, wobei der gespiegelte invertierte „Fingerabdruck“ durch die Farbe Rot hervorgehoben ist:
1 1 -1 1 1 -1 -1 1 1 1 -1 -1 1 -1 -1
In der Größenfolge zum Axiom L0 lässt sich entsprechend das Fragment so einordnen:
0 1 2 1 2 3 2 1 2 3 4 3 2 3 2 1
Hier ist also der Größenindex zur ersten Diatomee von links gleich 0, der größte auftretende Index beträgt 4. Die Übereinstimmung zwischen beobachtetem und berechnetem Muster ist überzeugend und belegt erneut das Gesetz von Pfitzer und MacDonald. Vor allem belegt sie die praktische Brauchbarkeit des D0L-Systems.
Anzahl der Übereinstimmungen der Muster
In Folge der Selbstähnlichkeit ist der Fingerabdruck der Differenzen in der nächsten Generation doppelt zu finden, und zwar zusätzlich gespiegelt und invertiert. Für das Fragment gibt es dann zwei Stellen mit Übereinstimmung. Um an der zweiten Stelle zu passen, muss es gespiegelt werden. Mit jeder Generation verdoppeln sich die Fundstellen. Erscheint das Muster des Fingerabdrucks erstmals in der Generation m, so findet man ihn in der Generation j mit j ≥ m genau 2j-m Mal. Die Unkenntnis der absoluten Zuordnung der Länge zu einem Größenindex führt also zu weiteren Möglichkeiten der Einordnung eines Fragments in die theoretische Größenfolge.
LINDENMAYER, A. (1968a). Mathematical models for cellular interactions, in development
I. Filaments with one-sided inputs. Journal of Theoretical Biology, 18, 290-299
Pfitzer, E. (1871) Untersuchungen über Bau und Entwicklung der Bacillariaceen (Diatomeen).
Botanische Abhandlungen 2, 1–189.
USSING, A.P., GORDON, R., ECTOR, L., BUCZKO´ , K., DESNITSKIY, A.G. & VANLANDINGHAM, S.L. (2005). The colonial diatom ‘‘Bacillaria paradoxa’’: chaotic gliding motility, Lindemeyer Model of colonial morphogenesis, and bibliography, with translation of O.F. Müller (1783), “About a peculiar being in the beach-water”. Diatom Monographs, Vol. 5. Koeltz, Koenigstein, Germany.
